Musical pitch is the building block of all things we hear. It determines how high or low a sound is. Pitch is to our ears, as are colors to our eyes. They breathe life into the sounds around us, like a tire screech or knock on the door, giving us clues to what is happening in our environment.
You may have heard of notes like A, G#, and Bb in Music Theory. Each of them carries a specific pitch that remains consistent between songs.
You may have also heard of A = 440Hz (Hertz). We will start by explaining Hertz.
How is Pitch formed?
Air is made up of particles.
Particles move about and vibrate.
Sound forms.
Pitch is formed by how fast air particles vibrate.
The faster the vibration, the higher the pitch. Vice Versa.
Frequency, measured in Hertz, is how many times something goes back and forth in a second. 440Hz is equivalent to a particle vibrating back and forth 440 times in a second!
One vibrating particle is not enough to create a sound that can be heard, but if you scale it up to a huge number of vibrating particles, it can be detected by our human senses.
Try out the slider below to hear the infinite possibilities of pitches! Fun fact – the lowest and highest pitches in the slider (20 – 20,000Hz) are the limits of our human hearing.
Origin of Pitch
On a piano, 12 distinct notes repeat from left to right (lower pitch to higher pitch). Each of these 12 notes and their variations carries a fixed frequency.
See the table below for a list of some of these frequencies.
| A4 | 440Hz (Standard Tuning) |
| B4 | 493.883Hz |
| C5 | 523.251Hz |
| D5 | 587.330 |
| E5 | 659.255 |
| F5 | 698.456 |
| G5 | 783.991 |
You may have a few questions when looking at this list.
- Why is A4 = 440Hz?
- Why are there 12 notes in each repetition?
- How do we determine the frequency of a note?
- Why are the frequencies in decimals?
All of these questions can be answered by looking at the history of pitch and how it was standardized. 2 concepts work in tandem for this to happen – Overtones and Equal Temperament.
Overtones Series (Harmonic Series)
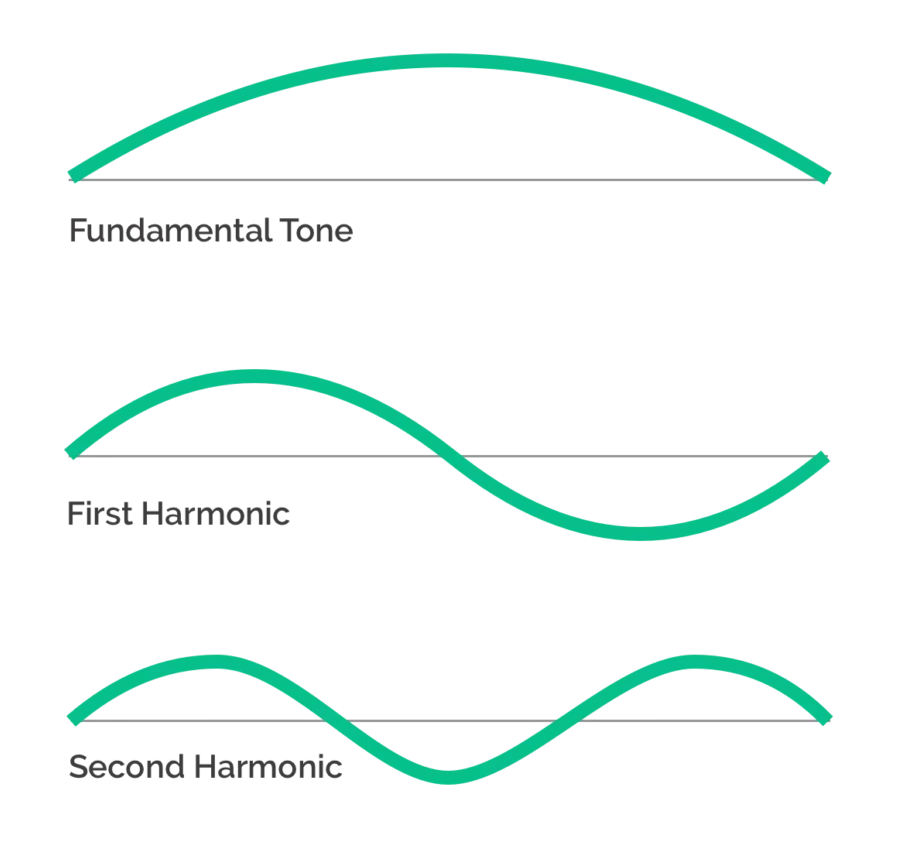
Natural sound is never one single pure frequency. The pitch generator above? Pure frequency via sine wave. Naturally occurring sounds eg. when you sing a note or blow a trumpet, are made up of a Fundamental Tone and smaller harmonically-related frequencies called Overtones.
Individual overtones are called harmonics. Each harmonic resonates at smaller ratios of the Fundamental Tone. As wavelengths get smaller, the frequency increases.
| Harmonic | Ratio of Wavelength | Frequency (Example) | Note (Example) | Interval to last |
|---|---|---|---|---|
| Fundamental | 1:1 | 55 Hz | A1 | Nil |
| 1st | 1:2 | 110 Hz | A2 | Octave |
| 2nd | 1:3 | 165 Hz | E3 | Perfect 5th |
| 3rd | 1:4 | 220 Hz | A3 | Perfect 4th |
| 4th | 1:5 | 275 Hz | C#4 | Major 3rd |
| 5th | 1:6 | 330 Hz | E4 | Minor 3rd |
| 6th | 1:7 | 385 Hz | G4 | Minor 3rd |
| 7th | 1:8 | 440 Hz | A4 | Major 2nd |
This is why many mathematicians in the olden days liked to associate Music with Maths.
This series of harmonics also forms naturally occurring intervals (distances between notes).
For example, playing the Fundamental Tone and 1st harmonic together will produce an octave. Playing the 1st harmonic and 2nd harmonic together will produce a Perfect 5th, and so on.
Most musicians agree that intervals are the most stable (clash the least) when played together up to the 4th harmonic. These intervals were highly sought after when tunings were being developed.
Listen to both samples below and note the differences between consonance (stable) and dissonance (unstable). The higher the instability, the more clashes (beatings) are present.
As harmonics get higher, intervals get shorter and dissonant. Past musicians have agreed on using pitches up to the 31st harmonic, giving us the 12 different intervals we know today in the Major Scale (approximately).
Fun Fact: The intensity of each overtone gives instruments their characteristic sound (Timbre)!
Equal Temperament
Why ‘approximately’? The Overtones Series poses some challenges. If we start tuning via overtones from 55 Hz (A1), playing in the key of A will be beautifully harmonious.
This tuning system is called Just Intonation.
However, venturing towards keys that are not A will sound dissonant because their ratios are not mathematically sound.
So then, musicians compromised.
First, you must understand that the Frequency Spectrum is logarithmic – it increases exponentially as we go up the spectrum.
You can see this in octaves where each next octave is achieved by multiplying by 2.
| Note | Frequency |
|---|---|
| A1 | 55 |
| A2 | 110 |
| A3 | 220 |
| A4 | 440 |
| A5 | 880 |
| A6 | 1760 |
| A7 | 3520 |
| A8 | 7040 |
Going from one note to another has to be in RATIOS instead of a fixed number. We cannot go 55Hz + 55Hz + 55Hz. It has to be 55Hz * (ratio).
What is this ratio? It is 12√2, ≈ 1.05946, a semitone.
How did we get here?
Simplified Explanation:
From 1 octave to the next, we know that the next octave is always twice the value. X is the initial frequency.
X –> 2X
12 intervals in an octave. We multiply X by a certain ratio (r) 12 times to reach the next octave. r * r * r * r …… = r12
X * r12 = 2X
By doing some simple algebra, we achieve the musical ratio.
r12 = 2X/X
r12 = 2
r = 12√2
This ratio (called the musical ratio) provides a healthy compromise between pure harmony and the freedom to modulate between all keys. Most musicians favored this tuning system.
This tuning system is called 12-tone Equal Temperament. And we still use 12TET today!
Conclusion
Now that you know the basic building blocks of music, we can explore intervals in the next post!